
|
Weiszfeld,
geometric median Computes the geometic
median of random 2D points |
|
|
| Points |
|
Number of points in region. |
| Width, height |
|
Region width and height. |
| Algorithm |
|
Algorithm to find g.-median. |
| Tolerance |
|
Convergence tolerance. |
| Minimization method |
|
| Trials (N), seed |
→ |
Monte Carlo trials, seed. |
| Simul. y-, x-axis bounds |
|
Simulation: axes bound in plot. |
| Plot points |
|
Simulation: n. of plot points. |
| Show values |
|
Show graph coordinates. |
Computes the geometric median,
(in a rectangular region) by minimum total distance (numerically):
either by multivariate minimization or by the Weiszfeld algorithm.
Shows the graphical results: #
(a) region with random points, and
centroid as larger circle and
g. median as smaller circle; and
(b) random behavior of simulated variable. |
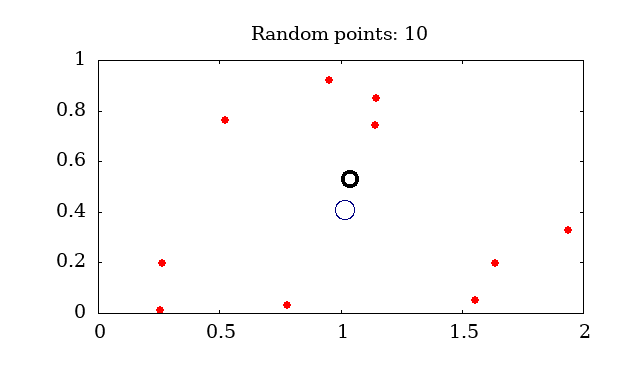 Fig. 1 |
|
| References: |
Plate: Weiszfeld |
• Optimization (scipy.optimize), The SciPy community.
• 'minimize' (methods)
• Vászonyi,
Andrew (Weiszfeld)
• The Dantzig Library (ORMS Today)
• CISTI'2026, 17–19 June (to be confirmed) 2026,
Santiago de Compostela (Spain).
• 1913-09-02: Gel'fand, Israil Moisyeevich
(Израиль Моисеевич Гельфанд)
(†2009-10-05, 96 yrs.). |



